How to Store and Retrieve Data from the Disk Efficiently

Irecently started reading Data Intensive Application by Martin Kleppmann, and it is one of the best books you can get your hands on. It talks about how data plays a vital role while building applications at scale. You can get a hold of a copy of the book here:

Data is the lifeblood of any modern application. Whether it is a web application, a mobile app, or desktop software, data is what makes it practical and valuable. But how do we store and retrieve data from the disk efficiently? How do we ensure that our data is consistent, reliable, and fast? How do we handle large amounts of data that cannot fit in the main memory?

In this article, we will explore some of the techniques and data structures used to efficiently store and retrieve data from the disk. We will learn about the challenges and trade-offs of working with data-intensive applications. We will also see some examples and diagrams to illustrate how these techniques work in practice.

We will cover the following topics:

• How to store data on the disk using an append-only log
• How to improve read performance using an index.
• How to reduce disk space using compaction and merging.
• How to use SSTables (Sorted String Tables) to store sorted data on the disk.
• How to use B-trees to create an index of an index for faster access.

Storing Data on the Disk Using an Append-only Log

The simplest way to store data on the disk is to append each record one after the other, sometimes called an append-only log. This means that whenever we want to write a new record to the disk, we go to the end of the file and write it there. This way, we avoid overwriting any existing data and ensure that our data is consistent even if the writing process gets interrupted or a power failure occurs.

For example, let's say we are a small startup that provides printing facilities. By doing so, we are required to collect a few pieces of information:

1. Name
2. Address
3. Content to Print (pdf, csv, doc, etc)

We can collect this information from a web form, but the issue is how we store it in the database.

The most straightforward way is to append each record one after the other, as shown below:

11, {name: "kishan", address: "bangalore", content: "pdf"},
22, {name: "max", address: "australia", content: "doc"},
33, {name: "mathew", address: "usa", content: "csv"},
44, {name: "chen", address: "china", content: "pdf"},

Notice we first gave a key (1, 2, 3, 4) and later followed up with its content. If someone wants to get the detail, all they need to provide us is a key.

Get me the details of key = 4. And we'll then go through each row one by one and return:

1  4, {name: "chen", address: "china", content: "pdf"}

If you wish to query on something else, you could have chosen any other value as your key, such as name, but there can be multiple rows with the same name. So, we decided to choose something unrepeatable.

The above method will work fast when we have to write to the database, as it only requires a sequential write operation. However, the challenge comes when we have to query for a particular record. It has to go through all the rows, which can be slow and inefficient.

Also, what if we edit the address of a person? Let's say Mathew shifted from the USA to Germany and wants to update his address. What will we do with this current setup?

11, {name: "kishan", address: "bangalore", content: "pdf"},
22, {name: "max", address: "australia", content: "doc"},
33, {name: "mathew", address: "usa", content: "csv"},
44, {name: "chen", address: "china", content: "pdf"},

We add one more row with the same key but different content:

13, {name: "mathew", address: "germany", content: "pdf"},

Notice we did not overwrite the previous row with key = 3. Instead, we appended a new row with the same key but updated content. When we search for key= 3, we will always give priority to the one that is present at the end of the file. In this way, we'll have the latest result.

But don't you think this will eventually be a bottleneck if our data keeps on growing? We will eventually run out of disk space, and the queries will take much longer time. How to deal with that?

Improving Read Performance Using an Index

To efficiently find the value for a particular key in the database, we need a different data structure: an index. An index is a data structure that helps queries return results faster. It is similar to a table of content that we find in almost all books. If you want to search for a particular chapter, you don't turn every page; you simply look in the table of contents at which page the chapter is present and directly head towards it.

An index only affects the performance of queries and not the content of the data itself. It is usually stored separately from the data file and contains pointers to the locations of the data records.

A simple index for our data file might look something like this:

1{
2"1": 0,
3"2": 64,
4"3": 278,
5"4": 122,
6}

We are using an in-memory HashMap, where the key is the actual key for our data (1, 2, 3, 4), and the value is the byte offset at which the record is present on the disk. For example, the record with key = 1 is at offset 0, which means it is at the beginning of the file. The record with key = 2 is at offset 64, which means it is 64 bytes away from the beginning of the file. And so on.

Notice the offset for key = 3 is 278 and not < 122. This is because we updated it earlier and appended a new record at the end of the file.

If we want to find the record with key = 3, we don't have to scan through the entire file. We can look up the index and get the offset as 278. Then we can jump to that offset on the disk and read the record from there. This way, we save a lot of time and disk seeks.

But having an index comes with a trade-off. It will speed up read queries, but every index will also slow down writes. This is because every time we write a new record to the disk, we also have to update the index accordingly. This adds an extra write operation and increases the complexity of concurrency and crash recovery.

Reducing Disk Space Using Compaction and Merging

Even if we have an index, we still have a problem of running out of disk space. This is because we are appending new records every time we update an existing record. This creates a lot of duplicate keys in our data file, which are no longer needed.

For example, let's say Mathew again changed his address from Germany to France. We will append another record with the same key but different content:

11, {name: "kishan", address: "bangalore", content: "pdf"},
22, {name: "max", address: "australia", content: "doc"},
33, {name: "mathew", address: "usa", content: "csv"},
44, {name: "chen", address: "china", content: "pdf"},
53, {name: "mathew", address: "germany", content: "pdf"},
63, {name: "mathew", address: "france", content: "pdf"},

Notice we have three records with key = 3, but only one of them is relevant (the last one). The other two are obsolete and can be discarded.

A good solution to reduce disk space is to break down the data file into segments of a certain size. After that, we can perform compaction on these segments. Compaction is a technique where we throw away duplicate keys in each segment and keep only the most recent update of each key.

But before breaking down the data file into segments, it would be better to include more duplicate keys in our data file to understand the compaction process better.

Let's assume Max changed his address from Australia to India, and Chen changed his address from China to Japan. We will append two more records with updated content:

1
21, {name: "kishan", address: "bangalore", content: "pdf"},
32, {name: "max", address: "australia", content: "doc"},
43, {name: "mathew", address: "usa", content: "csv"},
54, {name: "chen", address: "china", content: "pdf"},
63, {name: "mathew", address: "germany", content: "pdf"},
73, {name: "mathew", address: "france", content: "pdf"},
82, {name: "max", address: "india", content: "doc"},
94, {name: "chen", address: "japan", content: "pdf"},

Now, let me illustrate the compaction process. Assume each segment consists of four records such that:

Segment 1:

1
21, {name: "kishan", address: "bangalore", content: "pdf"},
32, {name: "max", address: "australia", content: "doc"},
43, {name: "mathew", address: "usa", content: "csv"},
54, {name: "chen", address: "china", content: "pdf"},

Segment 2:

1
23, {name: "mathew", address: "germany", content: "pdf"},
33, {name: "mathew", address: "france", content: "pdf"},
42, {name: "max", address: "india", content: "doc"},
54, {name: "chen", address: "japan", content: "pdf"},

Notice only segment 2 contains duplicate keys. The compaction process won't be able to compact any further in the case of segment 1 as it doesn't have any duplicate keys, but in the case of segment 2, it will return:

Segment 2 (Compacted)

1
23, {name: "mathew", address: "france", content: "pdf"},
32, {name: "max", address: "india", content: "doc"},
44, {name: "chen", address: "japan", content: "pdf"},

Notice it removed 3, {”name”: “mathew”, address: "germany", content: "pdf"}, as it is no longer needed. We can go further by combining Segment 1 and Segment 2 to check for duplicate keys among them.

After combining those, we get the following:

11, {name: "kishan", address: "bangalore", content: "pdf"},
22, {name: "max", address: "india", content: "doc"},
33, {name: "mathew", address: "france", content: "pdf"},
44, {name: "chen", address: "japan", content: "pdf"},

Note that the values after compaction are the latest; thus, older data can be discarded, thus saving us disk space.

The merging and compaction of segments can be done in a background thread, and while it is going on, we can still continue to serve read and write requests as normal.

You might ask, why not update the value in place?

1. Because appending and segment merging are sequential write operations, which are generally faster than random writes.
2. Concurrency and crash recovery are much simpler if segment files are append-only because we then don't have to worry about the case where a crash happened while a value was being overwritten. This might lead to the data being in an inconsistent state.

Even if we have introduced compaction and merging, if the number of records is in billions, how will it be feasible for us to maintain its index?

Keeping billions of distinct keys in memory for indexing is not optimal. Can we do something better?

Using SSTables (Sorted String Tables) to Store Sorted Data on the Disk

This is where SSTables come into the picture. SSTable stands for Sorted String Table. The idea is to sort the keys as they come. Now you may ask how one can keep a sorted table. There are plenty of techniques, and one of them is using red-black trees or AVL trees. With these data structures, you can insert the keys in any order and read them back in sorted order.

But how will sorted keys help? Let me explain. Now in order to find a particular key in the file, you no longer need to keep an index of all the keys in memory. For example, say you are looking for a key = 90, but you don't know the exact offset of that key in the segment file. However, you do know the offsets for the keys 20 or 125, and because of the sorting you know that k = 90 must appear between those two. This means you can jump to the offset of 20 and scan from there until you find the record with k = 90. You will scan from the 560th offset till the 1245th offset in this case.

Since the records are first sorted and then saved to the disk, the offsets also reflect that.

1{
2	"1": 0,
3	"2": 64,
4	"3": 123,
5	"4": 250,
6	"20": 560,
7	"125": 1245
8}

You still need an in-memory index to tell you about the offsets for some of the keys, but it can be sparse: one key for every few kilobytes of a segment file is sufficient.

Is there any other technique? To your surprise, it is the most widely used indexing structure called the B-tree.

Using B-trees to Create an Index of Index for Faster Access

It would be wise to know how data is stored or retrieved from disk to understand the philosophy behind B-trees.

If you have seen the inside of a hard disk, it consists of four most important things:

1. A magnetic disk (platter)
2. An Arm (read/write arm)
3. An Actuator
4. A Spindle

Let's first dissect the disk:

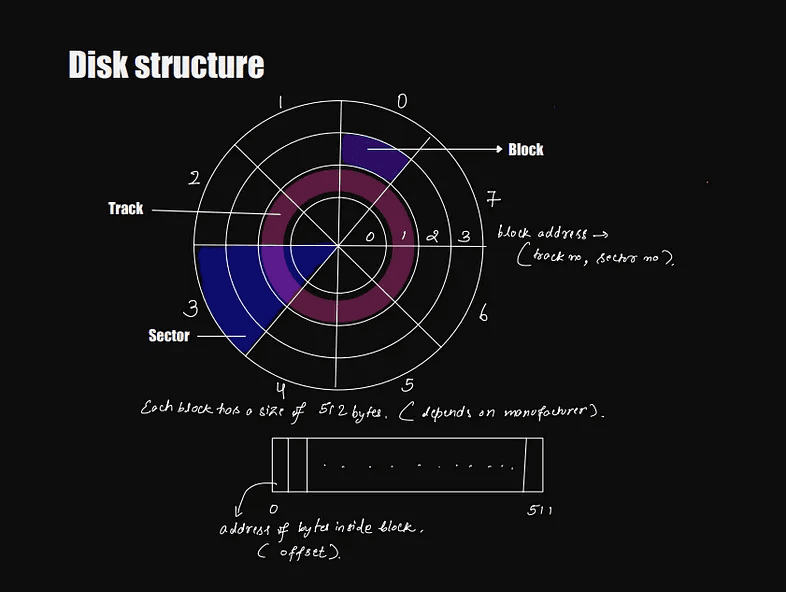
Disk Structure

A disk is divided into sectors and tracks. The intersection of the sector and track is termed a block. Each block can have a size; let's say, in our case, it is 512 bytes. Which means a block in our disk can store 512 bytes of data.

Let's say you want to write the data to the disk; you will have to provide two pieces of information: the sector and the track. After saving, say you want to know the content of the 10th byte inside that block. You'll have to first provide the block address and then will need to add the offset to it.

Let's say we want to store the above data on our disk. For this, I have defined how much space each data will take.

1id: 6 bytes
2name: 50 bytes
3address: 100 bytes
4content: 100 bytes

Thus, each record in our table will take (6 + 50 + 100 + 100) = 256 bytes of data.

As mentioned earlier, we store data in blocks. In our case, the block can hold a max of 512 bytes. How many records can a block save?

1(512 / 256) ⇒ 2 records

Let's say we have 100 records; how many blocks do you think we will need?

1(100 / 2) ⇒ 50 blocks

We'll need 50 blocks to store the complete data (100 records). Let's say we want to search for a particular record (row); how will we do it efficiently?

It depends on how fast our disk can spin and how quickly our blockhead can transition. When a disk spins, we change the sector; when the blockhead moves, we change the track. So by combining these two, we can move to any block within a track that is further within a sector.

We'll have to go through 50 blocks to search for a particular record. Can we reduce this access?

We'll store the block address corresponding to each. id.

11 → block_addr_1
22 → block_addr_1
33 → block_addr_2
4.
5.
6100 → block_addr_50

So, if somebody wants to search for key = 3, we will first go to the index and look for the corresponding pointer and directly jump to it. This way, we save valuable time.

But where do we store this index?

We store it on the disk itself at some block. But how much space will the index itself take? Notice it only holds two things: the id and its corresponding block address. Let's say these two field takes the following space:

1id → 6 bytes
2block_addr_i → 10 bytes

Now, each entry will take → 16 bytes. Since we had 100 records, how many blocks will we need to store this information?

1(1600 / 512) ~ 4 blocks

Earlier, in order to search for a particular record, we had to access all 50 blocks. After having an index, we need to search across the complete index, which is, say 4 blocks, and after that, we need to search the block that contains our data. So, in total, we had to search 5 blocks which are 10 times less than 50 blocks.

Can we further improve this? Yes, we can by employing one more index on top of it.

But this time, instead of having unique entries for every other index, we'll have a range. But why not employ the previous technique? Because if we have unique entries, then the total number of records will be 100, which will take the same amount of space and thus won't make any difference.

This index will point to the address of the previously created index. Makes sense?

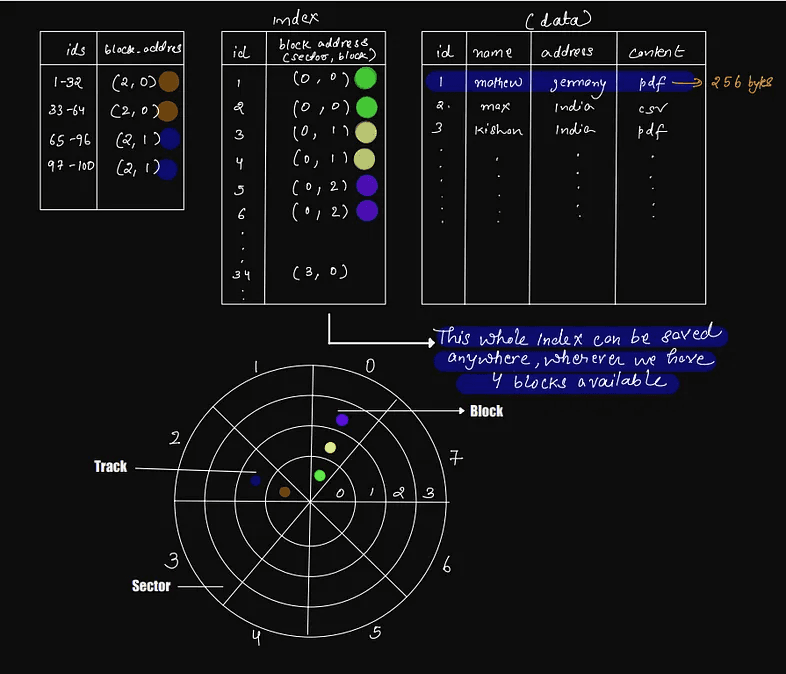
Index of Index

Since each row or record of the previous index took 16 bytes, this means each block can contain (512 / 16) = 32 index elements.

So, now our new index of an index will look something like the following:

1(1–32) → block_addr_index_1
2(33–64) → block_addr_index_2
3(65-96) → block_addr_index_3
4(97-100) → block_addr_index_4

Notice the new index only contains 4 entries, whereas the previous index contains 100 entries.

How will the search work now?

Let's say we want to search for key = 65; we'll look into the index of an index, which will give us the address (2, 1) i.e., the address where the chunk of the first level index is stored, then we will look at that index to get the pointer to the block address of the content on disk. So total, how many disks block access? Three from 5.

This way, we have created an index of an index, which will help us to find the block address of the original index faster. We can repeat this process until we have a single block that contains the top-level index. This is the basic idea behind B-trees, which are widely used to efficiently store and retrieve data from the disk.

The advantage of using B-trees is that they reduce the number of disk accesses required to find a particular record. This is because each node in a B-tree can store many keys and pointers, meaning the tree's height is relatively small. For example, if each node in a B-tree can store 100 keys and pointers, then a B-tree with 100 million records will have a height of only 3. This means that we only need to access 3 blocks on the disk to find any record in the tree.

B-trees are also dynamic data structures that can grow and shrink as records are inserted or deleted. They maintain their balance by splitting or merging nodes as needed. This ensures that the performance of the B-tree does not degrade over time.

Conclusion

In this article, we have learned how to store and retrieve data from the disk efficiently using various techniques and data structures. We have seen how to use an append-only log, an index, compaction and merging, SSTables, and B-trees to improve the performance and reliability of our data-intensive applications. We have also seen some examples and diagrams to illustrate how these techniques work in practice.

I hope that this article has been informative and helpful to you. If you want to learn more about data-intensive applications, I recommend you to read the book [Data Intensive Applications] by Martin Klepminn, which covers these topics in more depth and detail.

Thanks a lot.